Nhìn lên bầu trời vào một đêm không trăng, trời quang, con người có thể thấy được hàng ngàn ánh sáng lấp lánh. Ẩn trong những ngôi sao rải rác đó là những hình dạng nhất định. Một con sư tử ở đây, một con gấu ở kia. Khả năng nhận ra hình dạng của sao là một điểm mạnh đồng thời cũng là điểm yếu. Isaac Newton đã nghiên cứu về dạng thức của các vật thể rơi và đưa ra định luật vạn vật hấp dẫn. Nhiều người cũng nhận ra điểm nổi trội trong kết quả đấu điền kinh của mình khi mang tất bẩn và và sau đó từ chối thay đôi tất mới. Trong tất cả các dạng thức của tự nhiên, làm thế nào chúng ta nhận ra được những quy luật đúng? Chỉ ra sự khác biệt vốn là sự táo bạo mang tính thực tế. Do đó, không ngạc nhiên nếu bạn muốn làm vậy, không giống như hình học, môn khoa học xuất hiện với tư cách là một tập hợp các bằng chứng, luận cứ và tiền đề của các nhà triết học khô khan, lý thuyết về tính ngẫu nhiên bắt nguồn từ tư duy quan tâm tới bùa chú và cờ bạc, các vấn đề mà ta sớm có thể tưởng tượng được với xúc xắc hoặc chất độc trong tay hay trong sách hoặc cuộn giấy da.

Lý thuyết ngẫu nhiên về cơ bản là những hiểu biết thông thường. Nhưng đây cũng là một lĩnh vực rất mơ hồ, một lĩnh vực mà các chuyên gia nổi tiếng thường mắc lỗi trong khi các con bạc vô danh lại tính toán rất đúng. Để có thể hiểu về sự ngẫu nhiên và vượt qua quan niệm sai của mình, bạn cần phải có cả kinh nghiệm lẫn tư duy thấu đáo. Do vậy, chúng ta sẽ bắt đầu hành trình với một số định luật xác suất cơ bản và những thách thức trong việc phát hiện, tìm hiểu và áp dụng chúng. Một trong những cuộc khảo sát kinh điển về nhận thức của con người từ những định luật này chính là thí nghiệm do bộ đôi đã từng làm sáng tỏ nhận thức sai của chúng ta, Daniel Kahneman và Amos Tversky. Hãy thoải mái tham dự và học hỏi bất cứ điều gì về trực giác xác suất của chính bạn.

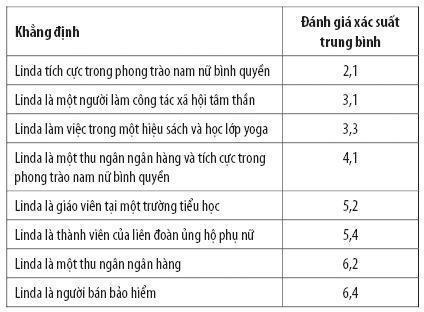
Giả sử có một phụ nữ tên Linda, 31 tuổi, độc thân, thẳng thắn, và rất thông minh. Trong trường đại học, chuyên ngành của cô là triết học và cô đặc biệt quan tâm tới sự phân biệt đối xử, công bằng xã hội và đã từng tham gia biểu tình chống hạt nhân. Tversky và Kahnenam trình bày vấn đề này cho một nhóm gồm 88 đối tượng và yêu cầu họ đánh giá những khẳng định sau theo thang điểm từ 1 đến 8 dựa trên xác suất xảy ra, với 1 là chắc chắn nhất và 8 là ít chắc chắn nhất. Và đây là kết quả, theo trật tự từ chắc chắn nhất tới ít chắc chắn nhất:

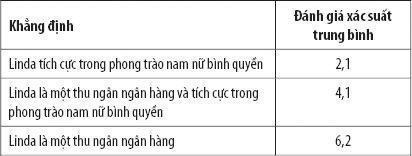
Thoạt nhìn, ta không thấy gì bất thường trong những kết quả trên. Trên thực tế, đoạn mô tả trên đại hiện cho hình ảnh một người đấu tranh về bình đẳng nam nữ và không đại diện cho một thu ngân ngân hàng hay người bán bảo hiểm. Nhưng bây giờ hãy chú ý vào chỉ ba trong số các xác suất và thứ tự trung bình của chúng được liệt kê ở bên dưới đây theo thứ tự từ chắc chắn nhất tới ít chắc chắn nhất. Đây là thứ tự mà 85% người được hỏi đã đánh giá ba xác suất này:

Nếu vẫn không thấy gì khác thường, thì Kahneman và Tversky hẳn đã lừa phỉnh bạn, vì nếu khả năng Linda là một thu ngân và người tích cực trong phong trào nam nữ bình quyền cao hơn khả năng Linda là một thu ngân, thì định luật đầu tiên của ta về xác suất, một trong những định luật cơ bản nhất, đã bị vi phạm: xác suất hai sự kiện cùng xảy ra không bao giờ lớn hơn xác suất mỗi sự kiện xảy ra riêng rẻ. Tại sao? Theo số học giản đơn: các khả năng sự kiện A xảy ra = các khả năng sự kiện A và B xảy ra + các khả năng sự kiện A xảy ra và sự kiện B không xảy ra.

Kahneman và Tversky không hề ngạc nhiên trước kết quả vì họ đã đưa cho những người tham gia rất nhiều xác suất, và mối quan hệ giữa ba viễn cảnh trên rất dễ bị quên mất khi xáo trộn. Và do đó họ đọc mô tả về Linda cho một nhóm khác, lần này họ chỉ đưa ra 3 xác suất:

Linda tích cực trong phong trào nam nữ bình quyền

Linda là một thu ngân ngân hàng và tích cực trong phong trào nam nữ bình quyền

Linda là một thu ngân ngân hàng

Thật ngạc nhiên, 87% đối tượng trong thí nghiệm này đánh giá xác suất Linda là thu ngân và tích cực trong phong trào nam nữ bình quyền cao hơn xác suất Linda là thu ngân. Và do vậy, nhóm nghiên cứu làm tiếp thí nghiệm: họ yêu cầu rõ ràng một nhóm 36 sinh viên tốt nghiệp loại khá cân nhắc câu trả lời cùng với định luật đầu tiên về xác suất. Thậm chí sau sự mách nước đó, hai trong số đối tượng vẫn trung thành với câu trả lời phi lôgic kia.

Điều thú vị mà Kahneman và Tversky chú ý tới là mọi người không mắc lỗi sai giống như vậy nếu bạn hỏi các câu hỏi không liên quan tới điều họ biết về Linda. Ví dụ, giả sử Kahneman và Tversky đã hỏi: khẳng định nào trong số những khẳng định sau đây đúng nhất:

Linda sở hữu quyền kinh doanh của International House of Pancakes.

Linda đã chuyển đổi giới tính và bây giờ tên là Larry

Linda đã chuyển đổi giới tính, bây giờ tên là Larry, và sở hữu quyền kinh doanh của International House of Pancakes

Trong trường hợp này, rất ít người cho rằng lựa chọn cuối chắc chắn hơn hai lựa chọn còn lại.

Kahneman và Tversky kết luận rằng vì chi tiết “Linda tích cực trong phong trào nam nữ bình quyền” phản ánh sự thật dựa theo mô tả lúc đầu về đặc điểm của cô, nên khi họ thêm chi tiết đó vào suy đoán thu ngân ngân hàng, nó sẽ làm tăng độ tin cậy của kịch bản. Nhưng rất nhiều điều có thể xảy ra giữa thời kỳ chống đối của Linda và thời kỳ cô ở tuổi 40. Cô ấy có lẽ đã tham gia vào một giáo hội theo trào lưu chính thống nào đó, kết hôn với một gã trọc đầu và xăm hình chữ thập ngược trên mông trái, hoặc quá bận rộn với các vấn đề của cuộc sống nên không còn tích cực với chính trị. Trong tất cả các trường hợp, cô ấy có lẽ đều đã không còn tích cực với phong trào bình đẳng nam nữ nữa. Do vậy, việc thêm chi tiết sẽ hạ thấp khả năng xảy ra kịch bản, ngay cả khi nó rõ ràng làm tăng khả năng chính xác.

Nếu những chi tiết chúng ta được cung cấp phù hợp với hình dung của ta về một điều gì đó, thì kịch bản càng nhiều chi tiết, nó càng giống thực tế và do đó ta thấy nó chắc chắn xảy ra nhất – thậm chí cho dù có được bổ sung thêm các chi tiết kém chắc chắn hơn. Sự mâu thuẫn giữa lôgic của xác suất với đánh giá của con người về những sự kiện không chắc chắn khiến Kahneman và Tversky thích thú, vì điều này có thể dẫn tới những đánh giá bất công hoặc sai lầm trong các tình huống thực tế. Điều nào chắc chắn hơn: một bị cáo, sau khi phát hiện thi thể, trốn khỏi hiện trường vụ án; hoặc một bị cáo, sau khi phát hiện thi thể, trốn khỏi hiện trường vụ án vì anh ta sợ bị kết tội giết người dã man? Việc tổng thống sẽ tăng trợ cấp giáo dục của liên bang hay việc ông ta/bà ta sẽ tăng trợ cấp giáo dục của liên bang bằng ngân sách cắt giảm nguồn trợ cấp của các bang khác chắc chắn hơn? Công ty bạn sẽ tăng doanh số bán hàng trong năm tới hay công ty sẽ tăng doanh số bán hàng trong năm tới vì tổng thể nền kinh tế đã có một năm kỷ lục chắc chắn hơn? Trong mỗi trường hợp, thậm chí ngay cả khi phần sau kém chắc chắn hơn phần đầu, thì nó cũng có vẻ dễ xảy ra hơn. Hoặc khi Kahneman và Tversky viết, “Một câu chuyện hay thường ít khả năng xảy ra hơn một câu chuyện ít thỏa đáng hơn… [giải thích].”

Kahneman và Tversky nhận ra thậm chí những bác sĩ được đào tạo trình độ cao vẫn mắc lỗi này. Họ trình bày với nhóm bác sỹ nội khoa về một vấn đề y tế nghiêm trọng: tắc mạch phổi (một cục máu nghẽn trong phổi). Nếu bị chứng bệnh này, bạn phải gặp một hoặc nhiều triệu chứng. Một số trong đó như liệt cục bộ, rất ít gặp; một số khác, như thở gấp, thường gặp hơn. Điều gì chắc chắn hơn: một bệnh nhân bị tắc mạch sẽ bị liệt cục bộ hay bệnh nhân sẽ bị cả liệt cục bộ và thở gấp? Kahneman và Tversky phát hiện 91% bác sỹ tin một cục máu nghẽn không chắc sẽ gây ra triệu chứng hiếm gặp đó bằng việc nó gây ra đồng thời cả triệu chứng hiếm gặp và triệu chứng thường gặp. (Theo lời biện hộ của các bác sỹ, các bệnh nhân không vào văn phòng của họ và nói những thứ đại loại như “Tôi có một cục máu nghẽn trong phổi. Hãy đoán các triệu chứng của tôi.”)

Vài năm sau, một sinh viên của Kahneman và một nhà nghiên cứu khác phát hiện ra rằng các luật sư cũng là nạn nhân do thành kiến trong đánh giá của mình. Dù là vụ hình sự hay dân sự, khách hàng thường phụ thuộc vào các luật sư để đánh giá về điều sẽ xảy ra nếu vụ của họ phải ra tòa. Đâu là cơ hội để trắng án hoặc thỏa hiệp hoặc đền bù theo nhiều mức khác nhau? Mặc dù các luật sư trình bày quan điểm bằng thuật ngữ của toán xác suất, nhưng họ vẫn đưa ra lời khuyên dựa trên dự báo cá nhân về tính chắc chắn tương đối của các kết quả có thể xảy ra. Cũng như vậy, ở đây các nhà nghiên cứu tìm ra rằng các luật sư quy xác suất cao hơn cho các khả năng được mô tả chi tiết hơn. Ví dụ, trong vụ kiện dân sự do nguyên đơn Paula Jones kiện tổng thống Bill Clinton, 200 luật sư đang hành nghề được yêu cầu dự đoán xác suất phiên tòa sẽ không diễn ra theo đầy đủ trình tự. Với một số người, xác suất được chia thành từng nguyên nhân cụ thể khiến phiên tòa có thể kết thúc sớm, như được thỏa hiệp, lời buộc tội được rút bỏ, tòa án bác đơn. Khi so sánh hai nhóm – những luật sư chỉ đơn giản được yêu cầu dự báo liệu phiên tòa có diễn ra đầy đủ không và những luật sư đã trình bày các khả năng phiên tòa có kết luật sớm – các nhà nghiên cứu nhận ra rằng các luật sư đã trình bày các khả năng phiên tòa có kết luận sớm chắc chắn nhiều hơn các luật sư chỉ dự báo phiên tòa sẽ kết thúc sớm.

Khả năng đánh giá các mối liên hệ có ý nghĩa giữa các hiện tượng khác nhau trong môi trường quan trọng đến mức ta phải xem xét thêm một vài hiện tượng nữa. Nếu một người thượng cổ đang chết đói nhìn vết mờ mờ màu xám lục trên một tảng đá ở xa, thì việc gạt bỏ ý nghĩ không mấy thú vị rằng thực tế đó chính là một con thằn lằn béo mẫm, ngon lành còn khó khăn hơn nhiều việc lao vụt tới và vồ lấy thứ hóa ra là mấy cái lá rụng. Và do vậy, đó là lý thuyết, chúng ta lẽ ra đã có thể tránh lỗi sai của người đi trước.

TRONG CÂU CHUYỆN về toán học, người Hy Lạp cổ đại nổi tiếng là người phát minh ra phương pháp của toán học hiện đại: qua các tiền đề, bằng chứng, định lý, thêm các tiền đề, bằng chứng, định lý… Tuy nhiên trong những năm 30 của thế kỷ XX, nhà toán học người Mỹ gốc Séc Kurt Gödel – một người bạn của Eistein – chỉ ra phương pháp này vẫn chưa đầy đủ: ông cho rằng đa số các định luật toán học đều mâu thuẫn hoặc chứa đựng những sự thật không thể chứng minh. Tuy vậy, sự phát triển của toán học vẫn tiếp diễn không ngừng như trường phái Hy Lạp, trường phái Euclid. Những người Hy Lạp, những thiên tài hình học, đã đưa ra những tiền đề nhỏ, những định đề được chấp nhận mà không cần chứng minh, và dùng chúng để chứng minh rất nhiều những định lý khác như tính chất của đường thẳng, mặt phẳng, tam giác, và những dạng hình học khác. Từ kiến thức này, họ phát hiện ra rằng trái đất hình cầu và thậm chí còn tính được cả bán kính của nó. Ai đó hẳn phải ngạc nhiên tại sao một nền văn minh có thể đưa ra một định lý như mệnh đề 29 trong Quyển 1 của bộ Tiên đề Ơ-cơ-lít – “một đường thẳng cắt hai đường thẳng song song sẽ tạo ra các góc so le bằng nhau, các góc đồng vị bằng nhau, và các góc trong cùng phía bằng hai góc vuông” – lại không thể đưa ra lý thuyết rằng nếu bạn ném hai lần xúc xắc, thì không dại gì mà đặt cược chiếc Corvette rằng cả hai lần đều được 6 điểm.

Thực tế, người Hy Lạp không những không có chiếc xe Corvette, mà họ cũng không có xúc xắc. Tuy nhiên, họ cũng đam mê cờ bạc. Họ có rất nhiều xác súc vật, nên họ chơi sấp ngửa bằng các xương xên, làm từ xương gót chân. Một xương xên có 6 mặt, nhưng chỉ 4 mặt vững chắc để khúc xương đứng vững được. Các học giả hiện đại lưu ý rằng do cấu tạo của xương nên cơ hội để khúc xương đứng bằng một trong 4 mặt này không bằng nhau: 10% cho hai mặt và 40% cho hai mặt còn lại. Trò chơi thông thường bao gồm tung 4 xương xên. Kết quả được quan tâm nhất là một trường hợp hiếm, nhưng không phải hiếm nhất: trường hợp mà cả bốn xương xên đứng trên 4 mặt khác nhau. Đó là cú ném Venus. Một cú ném Venus có xác suất khoảng 384/10.000, nhưng người Hy Lạp không biết điều đó, do không biết đến lý thuyết ngẫu nhiên.

Người Hy Lạp còn sử dụng xương xên khi đặt câu hỏi cho nhà tiên tri. Nhà tiên tri sẽ trả lời rằng đó là lời thánh truyền. Những người Hy Lạp lỗi lạc đã có nhiều lựa chọn quan trọng dựa trên lời khuyên của nhà tiên tri, bằng chứng rút ra từ những ghi chép của nhà sử học Herodotus, và các tác giả như Homer, Aeschylus, và Sophocles. Nhưng bất chấp tầm quan trọng của việc tung xương xên trong cờ bạc và tôn giáo, người Hy Lạp không mất công tìm hiểu những quy tắc của các cú ném xương xên.

Tại sao người Hy Lạp không xây dựng lý thuyết xác suất? Một câu trả lời là rất nhiều người Hy Lạp tin rằng tương lai mở ra theo ý các vị thần. Nếu kết quả tung xương xên nghĩa là “hãy cưới cô gái Sparta chắc nịch đã ghìm chặt ngươi trong trận đấu vật sau giờ học ở trường,” thì một cậu bé Hy Lạp sẽ không coi cú tung đó là kết quả may mắn (hoặc không may) của một quá trình ngẫu nhiên; cậu sẽ coi đó là ý của các vị thần. Từ quan điểm như vậy, việc tìm hiểu tính ngẫu nhiên sẽ không còn phù hợp. Do đó phép dự đoán sự ngẫu nhiên dường như không thể. Một câu trả lời khác nằm trong triết lý khiến người Hy Lạp trở thành những nhà toán học vĩ đại: Họ tuyên bố những chân lý tuyệt đối, được chứng minh bằng lôgic và các tiền đề, và không tán thành những tuyên bố không chắc chắn. Ví dụ, trong tác phẩm Phaedo của Plato, Simmias nói với Socrates “các luận cứ từ những khả năng là những kẻ lừa đảo” và lường trước công trình của Kahneman và Tversky khi chỉ ra “trừ phi cực kỳ cẩn trọng khi vận dụng chúng, chúng có khả năng khiến ta lầm lẫn – trong hình học, và trong những việc khác nữa.” Và trong Theaetetus, Socrates nói rằng bất cứ nhà toán học, “biện luận bằng xác suất và các khả năng xảy ra trong hình học, người đó đều không xứng đáng là ưu tú.” Nhưng ngay cả những người Hy Lạp tin rằng những cá nhân theo thuyết xác suất là những người ưu tú đi chăng nữa, thì họ cũng rất khó tìm ra một lý thuyết chắc chắn trong thời đại mà việc giữ gìn các bản ghi chép chưa trở nên phổ biến bởi con người có trí nhớ rất kém khi phải thống kê tần suất – rồi đến xác suất – của những gì xảy ra trong quá khứ.

Điều gì phổ biến hơn: số lượng từ tiếng Anh có 6 chữ cái có chữ cái thứ năm là n hay số lượng từ tiếng Anh tận cùng bằng ing? Đa số người được hỏi chọn nhóm từ tận cùng bằng ing. Tại sao? Vì từ tận cùng bằng ing dễ nghĩ ra hơn các từ có 6 chữ cái có chữ n là chữ cái thứ năm. Nhưng bạn không phải tra từ điển tiếng Anh của Oxford – hoặc thậm chí không cần biết cách tính – để chứng minh phát đoán trên sai: nhóm từ có sáu chữ cái có chữ cái thứ năm là n bao gồm tất cả những từ có 6 chữ cái tận cùng bằng ing. Các nhà tâm lý học gọi lỗi sai này là thành kiến vốn có bởi vì khi tái hiện lại quá khứ, chúng ta đặt ký ức (đa phần là ký ức mạnh) ở tầm quan trọng không thích đáng và từ đó sẵn sàng triệu hồi nhất.

Điều khó hiểu về thành kiến vốn có chính là việc nó âm thầm bóp méo quan điểm về thế giới bằng cách bóp mép nhận thức của ta về các sự kiện và môi trường trong quá khứ. Ví dụ, những người có xu hướng đánh giá quá cao tỷ lệ người vô gia cư bị bệnh thần kinh bởi vì khi họ gặp một người vô gia cư không cư xử bất thường, họ không chú ý và không kể với bạn bè về một người vô gia cư chẳng có gì đáng lưu ý mà họ gặp. Nhưng khi họ chạm trán một người vô gia cư giậm chân thình thịch xuống đường và vẫy tay với người bạn tưởng tượng đồng thời hát hò ầm ĩ, họ sẽ nhớ sự việc đó. Nếu có năm hàng dài người chờ thanh toán ở một của hàng tạp hóa thì khả năng bạn chọn xếp hàng tại hàng dài nhất là bao nhiêu? Trừ phi bạn đang bị lời nguyền của một phù thủy hắc ám, câu trả lời là từ 1 đến 5. Do vậy, tại sao khi bạn nhìn lại, bạn có cảm giác mình có năng khiếu phi thường trong việc chọn hàng dài nhất? Bởi vì bạn có nhiều thứ quan trọng để quan tâm hơn khi mọi việc diễn ra bình thường, thế nhưng chắc chắn bạn sẽ ấn tượng khi một phụ nữ trước mặt bạn chỉ có duy nhất một món đồ trong xe đẩy tranh cãi tại sao cô ta phải trả 1.50 đô-la cho con gà mà cô ta chắc chắn rằng cái biển ở quầy thịt ghi là 1.49 đô-la.

Một ví dụ về tác động của thành kiến vốn có tới phán xét qua quyết định của chúng ta là của một bồi thẩm đoàn trong một phiên tòa giả. Trong nghiên cứu này, bồi thẩm đoàn được cung cấp một lượng chứng cứ buộc tội bằng nhau và bào chữa liên quan tới trường hợp một lái xe say rượu khi anh ta đâm vào một chiếc xe chở rác. Bẫy đưa ra là một nhóm hội thẩm được cung cấp bằng chứng bào chữa theo kịch bản “nhợt nhạt”: “khi được chất vấn thì người chủ xe rác này khẳng định rằng chiếc xe của anh ta rất khó nhìn thấy trong đêm vì nó có màu xám.” Một nhóm khác được cung cấp bản ‘sống động’ của những bằng chứng giống y như vậy: “khi được chất vấn thì người chủ chiếc xe rác khẳng định chiếc xe của anh ta rất khó nhìn thấy trong đêm vì nó có màu xám. Người chủ này cũng lưu ý chiếc xe có màu xám ‘bởi vì nó che đi các vết bẩn. Ông muốn gì, tôi nên sơn nó màu hồng?’” Bằng chứng buộc tội cũng được trình bày theo hai cách, lần này bản “sống động” được trao cho nhóm đầu tiên và bản “nhợt nhạt” được trao cho nhóm thứ hai. Khi các bồi thẩm được yêu cầu đưa ra đánh giá mức độ có tội/vô tội, bên có phần mô tả chứng cứ “sống động” hơn luôn thắng thế, và tác động của thành kiến vốn có được củng cố hơn khi thời gian đình xử là 48 giờ trước khi đưa ra phán quyết cuối cùng (có lẽ do thời gian hồi tưởng mất nhiều).

Bằng cách bóp méo cái nhìn của chúng ta về quá khứ, các thành kiến vốn có làm phức tạp thêm bất cứ nỗ lực tìm hiểu nào. Đó từng là sự thật đối với người Hy Lạp cổ đại cũng như đối với chúng ta. Nhưng có một trở ngại lớn khác đối với lý thuyết xác suất sơ khai, một trở ngại rất thực tế: mặc dù xác suất cơ bản chỉ yêu cầu kiến thức số học, người Hy Lạp không biết về số học, hoặc ít nhất số học dưới dạng dễ dàng sử dụng. Ví dụ, tại Athens vào thế kỷ thứ V trước Công nguyên, thời kỳ đỉnh cao của nền văn minh Hy Lạp, muốn viết số người ta sử dụng một loại mã chữ cái alphabet. Chín chữ cái đầu tiên trong 24 chữ cái của bảng chữ cái Hy Lạp tượng trưng cho những con số từ 1 đến 9. Chín chữ cái tiếp theo tượng trưng cho các số mà ta gọi là 10, 20, 30… Và sáu chữ cái cuối cùng cộng thêm ba ký hiệu bổ sung tượng trưng cho 9 hàng trăm đầu tiên (100, 200, 300… cho tới 900). Nếu bạn nghĩ bạn có vấn đề với số học hiện nay, hãy thử trừ ΩΨΙΙ cho ΔΓΘ! Tệ hơn, thứ tự để viết các đơn vị, hàng chục, hàng trăm không rõ ràng. Hàng trăm lúc thì viết trước, lúc thì viết sau, và đôi khi người ta còn chẳng quan tâm đến thứ tự. Và điều tệ hại nhất có lẽ là, người Hy Lạp không có số 0.

Khái niệm số 0 đến Hy Lạp khi Alexander xâm chiếm đế chế Babylon năm 331 trước Công nguyên. Thậm chí ngay cả khi thời kỳ Alexander bắt đầu sử dụng số 0 để biểu thị sự vắng mặt của một số, nó cũng không được sử dụng với tư cách là một số theo đúng nghĩa. Trong toán học hiện đại, số 0 có hai thuộc tính chính: trong phép cộng nó là số mà khi cộng vào bất cứ số nào khác thì số đó không đổi, và trong phép nhân thì nó là số mà khi nhân với bất cứ số nào khác, chính nó không đổi. Khái niệm này không được đưa ra cho tới thế kỷ thứ IX, bởi một nhà toán học người Ấn Độ Mahāvīra. 

Thậm chí sau khi phát triển hệ thống chữ số hữu dụng, người ta còn mất nhiều thế kỷ trước khi công nhận phép cộng, phép trừ, phép nhân và phép chia là các phép tính cơ bản của số học – và chậm chạp nhận ra rằng các ký hiệu tiện dụng ấy sẽ khiến thao tác của họ dễ dàng hơn nhiều. Do đó chỉ tới thế kỷ XVI, người phương Tây mới sẵn sàng xây dựng lý thuyết xác suất. Tuy nhiên, bất chấp sự phiền hà của hệ thống tính toán rắc rối, chính nền văn minh đã thôn tính Hy Lạp – đế chế La Mã – là những người đặt bước tiến đầu tiên trong việc nghiên cứu về xác suất.

NGƯỜI LA MÃ nói chung khinh thường toán học, chí ít là toán học của người Hy Lạp. Theo lời người phát ngôn của La Mã, Cicero (106 – 43 trước Công nguyên), “Người Hy Lạp nắm giữ hình học đỉnh cao, do đó ở họ không gì phát triển rực rỡ hơn toán học. Nhưng chúng ta đã thiết lập tính ứng dụng của nó trong tính toán và đo lường như là tính hạn chế của môn khoa học này.” Thực sự, trong khi ai đó có thể tưởng tượng một cuốn sách giáo khoa của người Hy Lạp sẽ hướng vào việc chứng minh sự đồng đẳng của các tam giác trừu tượng, thì một cuốn sách giáo khoa Lã Mã thông thường tập trung vào những vấn đề như là làm thế nào để tính chiều rộng của một con sông khi kẻ thù chiếm đóng ở bờ bên kia.. Với những ưu tiên về toán học như vậy, chúng ta không ngạc nhiên khi người Hy Lạp sản sinh ra những thiên tài toán học như Archimedes, Diophantus, Euclid, Eudoxus, Pythagoras và Thales; trong khi người La Mã không có nổi một nhà toán học. Văn minh La Mã tiêu biểu ở sự sung túc và chiến tranh, không phải chân lý và cái đẹp. Điều này chính xác bởi vì khi quan tâm đến tính thực tế, người La Mã đã nhìn ra giá trị của việc tìm hiểu về xác suất. Do vậy, bởi không coi trọng hình học trừu tượng, Cicero đã viết rằng “xác suất gần như là kim chỉ nam của cuộc sống.”

Cicero có lẽ là người cổ đại xuất sắc nhất về xác suất. Ông sử dụng nó để biện luận cho các cách hiểu thông thường thắng bạc là do sự can thiệp của các đấng siêu nhiên. Ông đã viết “những tay chơi thường xuyên thỉnh thoảng sẽ gieo được cú Venus: do đó bây giờ hoặc sau này anh ta sẽ thực hiện được hai hay thậm chí ba lần thành công. Liệu chúng ta có trở nên kém hiểu biết đến mức quả quyết những việc như thế là do sự can thiệp của thần Venus, chứ không phải thuần túy do may mắn?” Cicero tin rằng một sự kiện có thể lường trước và tiên đoán được cho dù nó xuất hiện do tình cờ. Ông thậm chí đã sử dụng luận cứ thống kê để chế giễu những người tin vào chiêm tinh học. Khó chịu với việc chiêm tinh học vẫn tồn tại và phát triển ngoài vòng pháp luật ở La Mã, Cicero viết trong Cannae  năm 216 trước Công nguyên: Hannibal dẫn đầu khoảng 50.000 quân Carthage và quân liên minh tiêu diệt phần lớn quân đội La Mã, tàn sát hơn 60.000 trong số 80.000 lính của La Mã. “Tất cả những người La Mã đã ngã xuống tại Cannae đều có cùng lá số tử vi?” “Ai cũng có một lá tử vi và tất cả chết giống nhau?” Cicero hẳn sẽ cảm thấy được động viên nếu biết rằng 2 nghìn năm sau, trên tạp chí Nature, một nghiên cứu khoa học về tính hợp lý của các tiên đoán chiêm tinh đồng ý với kết luận của ông. Ngược lại, tờ New York Post ngày nay lại khuyên rằng là một người có cung Nhân Mã, tôi phải nhìn nhận các phê bình một cách khách quan và thực hiện bất cứ thay đổi nào nếu cần thiết.

Cuối cùng, di sản quan trọng của Cicero về xác suất chính là thuật ngữ mà ông đã sử dụng probabilis, đó là khởi nguồn của thuật ngữ chúng ta sử dụng ngày nay. Nhưng chính phần Digest, một phần của bộ Luật La Mã do hoàng đế Justinian soạn thảo vào thế kỷ thứ VI, là văn bản đầu tiên mà xác suất xuất hiện với tư cách một thuật ngữ quen thuộc của khoa học. Để cảm ơn người La Mã đã đưa các ứng dụng toán học thành lý thuyết hợp pháp, ta phải hiểu về nội dung: Luật La Mã trong thời kỳ Trung Cổ dựa trên tục lệ của các bộ lạc Giéc-manh. Chúng không thú vị lắm. Ví dụ, các quy tắc về chứng cớ. Tính trung thực của một người chồng khi phủ nhận việc ngoại tình với người may áo choàng của vợ sẽ được phán quyết không phải bằng khả năng người chồng có thể chịu đựng được lời châm chọc gai góc của thầy cãi bên nguyên mà bằng khả năng nhất quán của anh ta ngay cả khi bị dùng hình bằng việc châm một thanh sắt nóng đỏ vào người. (áp dụng lại tập tục đó và bạn sẽ thấy rất nhiều vụ ly hôn sẽ được dàn xếp mà không phải ra tòa). Và nếu bị cáo nói chiếc xe ngựa không hề phanh lại nhưng nhân chứng nói dấu móng cho thấy cái phanh đã được đạp, thì quan tòa –German sẽ đưa ra phán quyết đơn giản: “Chọn ra mỗi bên một người để chiến đấu bằng khiên và mác. Ai thua sẽ là kẻ nói dối và sẽ bị chặt tay phải.”

Tuy nhiên, cần bổ sung thêm, với thực tiễn của bộ lạc chiến đấu, người La Mã kiếm tìm trong tính chính xác của toán học một phương pháp khắc phục những thiếu sót trong đế chế già nua và chuyên quyền của mình. Nhìn vào bối cảnh, quan điểm của người La Mã về công lý sử dụng những thuật ngữ rất tiến bộ. Họ nhận ra chứng cớ và bằng chứng thường xung đột nhau và cách tốt nhất để giải quyết xung đột đó là lượng hóa sự không chắc chắn có thể xảy ra. Người La Mã đưa ra khái niệm minh chứng nửa vời để áp dụng vào trường hợp mà không có lý do thuyết phục để tin hay không tin vào bằng chứng hoặc chứng cớ. Trong một số trường hợp bằng chứng của bản án La Mã bao gồm các mức độ chứng minh, như trong một sắc lệnh nhà thờ “một giám mục sẽ không bị kết tội nếu không có 72 nhân chứng… một hồng y giáo chủ sẽ không bị kết tội nếu không có 44 nhân chứng, một người trợ tế của thành Rome sẽ không bị kết tội nếu không có 36 nhân chứng, một phó trợ tế, thầy dòng, thầy phù thủy, giáo sĩ, hoặc người giữ cửa sẽ không bị kết tội nếu không có 7 nhân chứng.” Để bị kết án theo các quy định đó, bạn sẽ vừa phải nhận tội vừa phải mời gọi mọi người làm chứng cho mình. Tuy nhiên, việc công nhận xác suất sự thật trong bằng chứng có thể thay đổi và các quy định kết hợp những khả năng xảy ra là một sự khởi đầu. Và chính tại một nơi nào đó của thành Rome cổ đại, hệ thống các quy định dựa trên xác suất đã xuất hiện đầu tiên.

Thật không may, rất khó đạt được độ linh hoạt về lượng khi bạn đang ở giai đoạn từ thế kỷ thứ VIII cho tới thế kỷ thứ XIV. Mặc dù luật La Mã đã có sự cấu kết hợp pháp và hợp lý, ở đây vẫn thiếu tính hiệu quả toán học. Ví dụ, trong Luật La Mã, hai minh chứng nửa vời hợp thành một minh chứng đầy đủ. Điều này nghe có vẻ hợp lý với những ai không quen tư duy định lượng, nhưng với những người đã quen với các phân số thời nay có thể đặt câu hỏi, nếu hai chứng minh nửa vời bằng một sự chắc chắn tuyệt đối, vậy ba chứng minh nửa vời thì sẽ cho ta điều gì? Theo phương pháp phức hợp xác suất đúng, không chỉ hai minh chứng nửa vời nhỏ hơn một sự chắc chắn tuyệt đối, mà cộng số lượng không hạn chế các chứng minh thành phần cũng không thể thành một chỉnh thể bởi vì để ghép các xác suất, bạn không cộng, mà bạn phải nhân.

Điều đó đem tới cho chúng ta quy luật tiếp theo. Quy luật về phức hợp xác suất: Nếu hai sự kiện có thể xảy ra, A và B, là độc lập, thì xác suất cả A và B cùng xuất hiện bằng tích của xác suất riêng của chúng. Giả sử một người đã kết hôn có thể ly dị trung bình 1 lần trong tổng số 50 cơ hội mỗi năm. Ngược lại, một cảnh sát có khoảng 1 trong 5.000 cơ hội mỗi năm bị giết khi làm nhiệm vụ. Vậy hãy tính số cơ hội mà một người cảnh sát có thể ly dị và bị giết trong cùng một năm? Theo quy tắc ở trên, nếu những sự kiện đó là độc lập, số khả năng sẽ khoảng 1/50 x 1/5.000 = 1/250.000. Tất nhiên 2 sự kiện này không độc lập, chúng có liên hệ: khi bạn chết, bạn không thể ly dị được nữa. Và do vậy, cơ hội để xảy ra điều tệ hại kia chắc chắn phải ít hơn 1/250.000.

Tại sao lại nhân thay vì cộng? Giả sử bạn làm một bộ bài từ những bức hình của 100 anh chàng bạn từng gặp gỡ qua dịch vụ hẹn hò trên mạng, những anh chàng trong các bức hình thường giống như Tom Cruise nhưng thực tế họ giống Danny Devito hơn. Giả sử, ở mặt sau của mỗi lá bài, bạn ghi các dữ liệu cụ thể về người đó, như chân thật (có hoặc không) và hấp dẫn (có hoặc không). Cuối cùng, giả sử tỷ lệ 1/10 cô bạn tâm giao đánh giá có với từng lá bài. Vậy bao nhiêu lá bài trong số 100 tấm qua được bài kiểm tra của cả 2 tiêu chí? Hãy lấy chân thật làm tiêu chí đầu tiên. Vì 1/10 lá bài có đánh có bên dưới tiêu chí chân thật, nên có 10 lá trong số 100 lá bài đạt yêu cầu. Trong 10 lá bài đó, bao nhiêu người hấp dẫn? Một lần nữa, 1/10, do đó bạn còn lại 1 lá bài. Tỷ lệ 1/10 đầu tiên làm giảm xác suất bằng 1/10, và tỷ lệ 1/10 tiếp theo cũng vậy, khiến kết quả là 1/100. Đó là lý do tại sao bạn phải nhân. Nếu bạn có thêm các điều kiện thay vì chỉ có 2 tiêu chí chân thật và hấp hẫn, bạn sẽ phải nhân tiếp, và…ồ, chúc may mắn.

Trước khi tiếp tục, ta cần lưu ý đến một chi tiết quan trọng: một mệnh đề rằng nếu hai sự kiện có thể xảy ra, A và B, là độc lập. Giả sử một chuyến bay chỉ còn 1 ghế trống và 2 hành khách lẽ ra phải có mặt. Giả sử, theo kinh nghiệm, hãng hàng không biết có 2/3 khả năng một hành khách đã đặt chỗ sẽ đến để làm thủ tục. Sử dụng quy tắc nhân, người soát vé có thể kết luận có 2/3 x 2/3 = 44% khả năng cô ta sẽ phải giải quyết người khách hàng không may mắn. Khả năng khách hàng sẽ không đến và chuyến bay sẽ phải khởi hành với một ghế trống là 1/3 x 1/3 = 11%. Nhưng giả sử các khách hàng độc lập. Nếu nói họ đi cùng nhau, thì phân tích ở trên là sai. Khả năng cả hai đều xuất hiện là 2/3, bằng với khả năng 1 người có mặt. Điều quan trọng ở đây là bạn phải phức hợp xác suất từ những xác suất đơn lẻ bằng cách nhân chỉ khi các sự kiện không liên quan đến nhau.

Nguyên tắc chúng tôi vừa áp dụng có thể áp dụng vào quy định chứng minh nửa vời của La Mã: khả năng mà hai chứng minh nửa vời độc lập đều sai là 1/4, do vậy hai chứng minh nửa vời hợp thành 3/4 của một chứng minh, không phải là một sự thật đầy đủ. Người La Mã đã dùng phép cộng ở chỗ đáng ra họ nên nhân. 

Có những tình huống mà các xác suất nên cộng với nhau, đó chính là quy luật tiếp theo. Nó xảy ra khi chúng ta muốn biết khả năng hoặc sự kiện này hoặc sự kiện kia xảy ra, ngược lại với tình huống ở trên – chúng ta muốn biết khả năng sự kiện này và sự kiện khác cùng xảy ra. Định luật này như sau: Nếu một sự kiện có nhiều khả năng xảy ra khác nhau và riêng biệt, A, B, C…, thì xác suất để A hoặc B xảy ra bằng tổng xác suất xuất hiện của A và B, và tổng các xác suất của tất cả các khả năng xảy ra (A, B, C…) là 1 (nghĩa là 100%). Khi bạn muốn biết khả năng hai sự kiện độc lập, A và B, cùng xảy ra thì bạn nhân; nếu bạn muốn biết khả năng một trong hai sự kiện xảy ra, A và B, thì bạn cộng. Trở lại với hãng hàng không kia, khi nào nhân viên soát vé nên cộng các khả năng thay vì nhân chúng? Giả sử cô muốn biết khả năng hoặc cả hai hành khách đều đến hoặc không hành khách nào đến. Trong trường hợp này cô nên cộng các xác suất riêng biệt, theo như chúng ta đã tính toán ở trên, để cho ra kết quả là 55%.

Ba quy luật đơn giản này tạo thành nền tảng của lý thuyết xác suất. Khi được ứng dụng đầy đủ, chúng sẽ giúp ta nhìn thấu đáo hơn bản chất của tự nhiên và thế giới xung quanh. Chúng ta luôn sử dụng chúng trong các quyết định hàng ngày. Nhưng giống như các nhà làm luật La Mã, chúng ta thường không sử dụng chúng đúng cách.

TA RẤT DỄ NHÌN LẠI, lắc đầu, và viết sách với tựa kiểu như Những người La Mã mục nát (Scholastic, 1994). Nhưng để chúng ta không trở thành tự mãn vô lý, tôi sẽ kết thúc chương này bằng cách nhìn khác về những quy luật mà tôi đã bàn tới. Nó đủ để thức tỉnh bất cứ ai đang say trong cảm giác văn hóa ưu việt.

Tin tốt lành là ngày nay chúng ta không có các chứng minh nửa vời. Nhưng chúng ta có loại chứng minh 999.999/1.000.000. Ví dụ, các chuyên gia về phân tích ADN không lạ với việc làm chứng tại một phiên tòa hình sự rằng một mẫu ADN lấy từ hiện trường vụ án chính là của nghi phạm. Sự phù hợp này đúng đến mức nào? Khi cứ chứng ADN lần đầu tiên được đưa ra, rất nhiều chuyên gia chứng nhận các kết quả dương tính sai lầm không thể xảy ra trong xét nghiệm ADN. Ngày nay, các chuyên gia ADN thường chứng nhận rằng khả năng một người ngẫu nhiên nào đó phù hợp với mẫu thử của tội phạm thấp hơn 1/1.000.000 hoặc 1/1.000.000.000. Với những trường hợp ngoại lệ đó, ta khó có thể trách bồi thẩm đoàn vì đã vứt chiếc chìa khóa quan trọng đi. Nhưng còn một thống kê khác không phải của bồi thẩm đoàn, người có liên quan tới số liệu sai mà phòng thí nghiệm đưa ra, ví dụ như khi thu thập và xử lý mẫu, do vô ý trộn lẫn hoặc tráo lẫn các mẫu, hoặc đọc nhầm hoặc đọc sai kết quả thử. Lỗi sai thường hiếm nhưng không hiếm như một sự phù hợp ngẫu nhiên. Phòng thí nghiệm tội phạm Philadelphia thừa nhận rằng họ đã bị tráo mẫu thử của bị đơn và nạn nhân trong một vụ cưỡng hiếp, và một hãng xét nghiệm tên là Cellmark Diagnostics cũng đã thừa nhận một lỗi tương tự. Không may, quyền lực của thống kê về ADN được đưa ra trước một phiên tòa ở Oklahoma đã khiến tòa kết tội một người đàn ông tên Timothy Durham tới hơn 3.100 năm tù mặc dù 11 nhân chứng đã gặp anh ta ở bang khác tại thời điểm xảy ra án mạng. Hóa ra trong phân tích lần đầu, phòng thí nghiệm đã không thể phân tách hoàn toàn ADN của tội phạm và nạn nhân trong dung dịch thử, và sự kết hợp giữa ADN của tội phạm và nạn nhân đã đem lại một kết quả dương tính khi so sánh với ADN của Durham. Lần thử sau này đã phát hiện ra sai lầm đó, và Durham được thả sau khi đã ở tù gần 4 năm.

Tỷ lệ các lỗi sai do nguyên nhân từ con người rất khác nhau, nhưng nhiều chuyên gia đánh giá nó ở khoảng 1%. Tuy nhiên, vì tỷ lệ lỗi sai của nhiều phòng thí nghiệm chưa bao giờ được xem xét, nên tòa án thường không cho phép chứng thực thống kê tổng thể này. Thập chí, nếu tòa án cho phép chứng minh kết quả dương tính sai, thì bồi thẩm đoàn làm thế nào để đánh giá? Đa số bồi thẩm cho rằng trong hai loại lỗi sai – 1/1.000.000.000 xác suất tình cờ trùng hợp và 1/100 xác suất sai do lỗi của phòng thí nghiệm – tỷ lệ sai sót tổng thể phải ở đâu đó ở giữa, cứ cho là 1/500.000.000, đa số các bồi thẩm đoàn không còn nghi ngờ gì. Nhưng sử dụng các quy luật xác suất, chúng ta sẽ có câu trả lời rất khác.

Hãy nghĩ rằng: do cả hai loại lỗi đều không chắc chắn, chúng ta có thể lờ đi khả năng đồng thời có cả lỗi tình cờ trùng hợp và lỗi của phòng thí nghiệm. Do đó, chúng ta đi tìm xác suất lỗi này hoặc lỗi kia xảy ra. Chúng ta dùng quy tắc cộng: xác suất xảy ra lỗi phòng thí nghiệm (1/100) + xác suất xảy ra lỗi tình cờ trùng hợp (1/1.000.000.000). Do lỗi sau nhỏ hơn lỗi trước 10 triệu lần, nên để có con số xấp xỉ đẹp, khả năng xảy ra cả hai lỗi bằng với khả năng xảy ra lỗi thường gặp hơn – nghĩa là các khả năng là 1/100. Với mỗi nguyên nhân có thể xảy ra, chúng ta nên bỏ qua chứng nhận buồn cười của chuyên gia về sai lệch của các trường hợp tình cờ trùng hợp và tập trung vào tỷ lệ sai sót trong phòng thí nghiệm – thông tin mà tòa án thường không cho phép các luật sư trình bày! Và do vậy những tuyên bố nhắc đi nhắc lại về tính chính xác của ADN là cường điệu hóa.

Đây không phải là vấn đề duy nhất. Công dụng của toán học trong hệ thống luật pháp hiện đại gặp phải những vấn đề nghiêm trọng không kém gì trong thời La Mã. Một trong những trường hợp nổi tiếng nhất minh họa công dụng và sự lạm dụng xác suất trong pháp luật là vụ Người dân và Collins, diễn ra năm 1968 tại Tòa án tối cao California. Đây là các số liệu về vụ án nêu trong quyết định của tòa:

Vào hồi 11.30 ngày 18 tháng 6 năm 1964, bà Juanita Brooks đi mua sắm trở về dọc theo một ngõ hẻm tại khu vực San Pedro, thành phố Los Angeles. Bà kéo đằng sau một giỏ liễu đan đựng tất cả các đồ tạp phẩm đã mua và để ví của mình lên trên cùng. Bà đang chống gậy. Khi bà cúi xuống để nhặt một hộp bìa cứng, đột nhiên bà bị đẩy ngã xuống đất bởi một kẻ lạ mặt. Bà bị choáng váng bởi cú ngã và thấy nhức nhối khắp người. Bà cố gắng ngước lên và thấy một người phụ nữ trẻ đang chạy khỏi hiện trường. Theo lời bà Brooks, người đó nặng khoảng 70 kg, mặc “thứ gì đó tối màu” và tóc màu “giữa màu vàng sáng và vàng đậm”, nhưng sáng hơn màu tóc của bị cáo Janet Collins khi bị cáo xuất hiện trước tòa. Ngay sau đó, bà Brooks phát hiện ví của bà, trong đó có còn khoảng 35 – 40 đô-la, đã bị mất.

Vào cùng khoảng thời gian với vụ cướp, John Bass, người sống ở cuối con hẻm đó, đang đứng trước cửa nhà tưới cỏ. Ông nghe thấy rất nhiều tiếng khóc và tiếng hét từ con hẻm. Khi ông nhìn theo hướng đó, ông thấy một phụ nữ chạy khỏi con hẻm và lao vào một chiếc ôtô màu vàng đậu bên kia đường. Ông không nhận dạng được chiếc xe. Chiếc xe nổ máy lập tức và vượt qua các phương tiện đang đỗ khác trên con hẻm nên nó băng qua ông Bass chỉ cách 2m. Do đó, ông nhìn thấy một người đàn ông da đen đang lái xe, để ria và râu quai nón… Rất nhiều nhân chứng khác mô tả chiếc xe màu vàng, màu vàng với nóc màu trắng nhạt, hoặc màu vàng với nóc màu trắng vỏ trứng. Chiếc xe còn được mô tả có kích cỡ từ trung bình tới lớn.

Một vài ngày sau sự việc ở Los Angeles, cảnh sát phát hiện ra một chiếc xe Lincoln màu vàng có nóc màu trắng nhạt đỗ trước nhà bị cáo và nói chuyện với họ, giải thích rằng anh ta đang điều tra một vụ cướp. Anh ta lưu ý rằng những người tình nghi phù hợp với mô tả về người đàn ông và người đàn bà trong vụ án, ngoại trừ việc người đàn ông không có râu quai nón, mặc dù anh ta thừa nhận đôi lúc anh ta cũng để râu. Sau hôm đó, cảnh sát Los Angeles đã bắt hai kẻ tình nghi, Malcolm Ricardo Collins, và vợ anh ta, Janet.

Các chứng cứ chống lại cặp đôi này không nhiều lắm, vụ án gặp khó khăn trong việc nhận dạng của nạn nhân và nhân chứng John Bass. Thật không may, bên nguyên không thể chứng minh về lời khai của nhân chứng, nạn không không nhận dạng được Janet là thủ phạm và cũng không nhìn thấy người lái xe. John Bass không nhìn thấy thủ phạm và nói tại đồn rằng ông ta không thể nhận dạng rõ ràng Malcolm Collins là người lái xe đó. Và do đó, dường như vụ án đang rơi vào ngõ cụt.

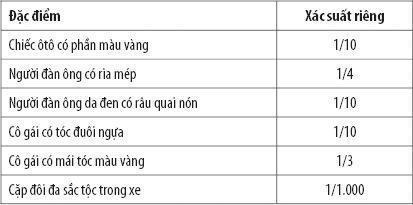
Ghi nhận về nhân chứng, mô tả của tòa án Tối cao California chỉ là “trợ giảng toán học tại một trường cao đẳng của bang”. Nhân chứng này đã chứng tỏ sự thật mà phần chứng (kẻ tình nghi là “một người phụ nữ Causasus với mái tóc đuôi ngựa màu vàng… [và] một người da đen với râu quai nón và ria mép” lái chiếc ôtô có phần màu vàng) đã đủ để kết tội cặp đôi kia. Để minh họa cho điều này, bị đơn sẽ được mô tả trong bảng theo đúng nguyên văn bản án của Tòa án tối cao:

Người trợ giảng toán học, theo yêu cầu của công tố, nói rằng quy tắc tích số áp dụng cho các số liệu này. Bằng cách nhân tất cả các xác suất, người ta kết luận rằng khả năng cặp đôi phù hợp với tất cả đặc điểm nhận dạng này là 1/12.000.000. Theo đó, anh ta nói, ta có thể suy ra khả năng cặp đôi này vô tội là 1/12.000.000. Công tố viên sau đó chỉ ra rằng xác suất riêng đã được ước tính và mời ban hội thẩm cho ý kiến và tính toán. Như anh ta nói, bản thân anh ta tin đó là cách ước tính thận trọng, và xác suất anh ta tính được nếu sử dụng các nhân tố anh ta giả định thì vào khoảng 1/1.000.000.000. Bồi thẩm đoàn đã chấp nhận kết luận này và kết tội cặp đôi kia.

Điểm sai ở đây là gì? Đối với một điều như chúng ta đã thấy, nhằm tìm ra xác suất phức hợp bằng cách nhân các xác suất thành phần, các tiêu chí phải độc lập, và trong trường hợp này rõ ràng chúng không độc lập. Ví dụ, bảng trên thể hiện khả năng “một người đàn ông da đen có râu quai nón” là 1/10 và “một người đàn ông có ria mép” là 1/4. Nhưng đa số đàn ông có râu quai nón thì cũng đều có ria mép, do đó nếu bạn thấy “một người đàn ông da đen có râu quai nón,” thì khả năng 1/4 về người đàn ông có ria mép sẽ không chính xác – xác suất phải cao hơn. Vấn đề có thể được giải quyết nếu bạn loại trừ tiêu chí “người đàn ông da đen có râu quai nón”, thì tích số của các xác suất sẽ giảm còn 1/1.000.000.

Còn một lỗi phân tích nữa: xác suất có liên quan không phải là xác suất nêu ở trên – tức xác suất rằng cặp đôi được chọn ngẫu nhiên sẽ khớp với mô tả về kẻ tình nghi. Tuy nhiên, xác xuất thích đáng là khả năng mà một cặp đôi khớp với tất cả các đặc điểm kia là cặp đôi có tội. Xác suất trước là 1/1.000.000. Nhưng với xác suất sau, dân số khu vực xung quanh vụ án xảy ra vào khoảng vài triệu, do đó bạn hoàn toàn có lý để kỳ vọng có 2 hoặc 3 cặp trong vùng khớp với các mô tả. Trong trường hợp đó, xác suất cặp đôi khớp với các mô tả là có tội, chỉ dựa trên chứng cứ này (hầu như là tất cả chứng cứ mà tòa có) chỉ là 1/2 hoặc 1/3. Vì những lý do này, tòa tối cao lật lại bản án của nhà Collins.

Công dụng của xác suất và thống kê trong phòng xử án hiện đại vẫn là một chủ đề được tranh cãi. Trong trường hợp của nhà Collins, Tòa án tối cao California chế nhạo cái được gọi là “xét xử bằng toán học,” nhưng nó đã mở cửa cho “những ứng dụng đầy đủ của công cụ toán học.” Trong các năm tiếp theo, các phiên tòa hiếm khi xem xét các tranh luận toán học, nhưng thậm chí khi luật sư hay thẩm phán không thích các luận cứ toán học hoặc xác suất rõ ràng, thì họ cũng thường sử dụng loại lý lẽ này, ví dụ như khi các thẩm phán cân nhắc chứng cứ. Hơn nữa, các luận điểm thống kê ngày càng trở nên quan trọng do sự cần thiết phải sử dụng các chứng cứ ADN. Thật không may, với tầm quan trọng ngày càng tăng như vậy nhưng sự hiểu biết của một bộ phận luật sư, thẩm phán hoặc bồi thẩm về vấn đề này không hề tăng. Như Thomas Lyon, một giáo sư về xác suất và luật tại trường Đại học Nam California đã giải thích, “rất ít sinh viên sử dụng xác suất vào quá trình làm luật, và rất ít luật sư thấy được tầm quan trọng của nó.” Trong lĩnh vực luật cũng như các lĩnh vực khác, hiểu biết về tính ngẫu nhiên có thể khám phá ra những ẩn ý của sự thật, nhưng chỉ với những người sở hữu các công cụ khám phá chúng. Trong chương tiếp theo, chúng ta sẽ tìm hiểu câu chuyện của người đầu tiên nghiên cứu về các công cụ này một cách  hệ thống.