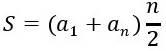(Ta-nhi-a gửi Số Không)

Số Không thân mến!

Bọn mình vẫn cứ quanh quẩn ở cái chỗ bị phù phép này.

Bọn mình dịch xong mật mã của bức thư liền bắt tay vào giải bài toán của vỏ đậu. Nghĩ nát óc mà không ra! Bọn mình đã toan đến hỏi máy tra cứu tự động, nhưng chữ P ngăn lại. Ông ta nói với giọng bí mật.

• Nếu quả các bạn muốn giúp đỡ một người chưa quen biết thì các bạn nên tự giải lấy bài toán này. Nhưng muốn thế thì phải lập phương trình…

Nói thì dễ đấy. Lập phương trình! Lập tam giác Pa-xcan còn chưa nên hồn nữa là lập phương trình!…

Chữ P tỏ vẻ thông cảm:

• Tôi hiểu. Vì các bạn chưa đến công trường xây dựng mẫu của chúng tôi đấy thôi. Chứ nếu đã đến đấy rồi thì chắc hẳn các bạn sẽ biết nên làm như thế nào.
• Xây dựng và phương trình ư? – Xê-va lắc đầu hỏi.
• Có gì đáng ngạc nhiên! Thế các bạn tưởng không có phương trình mà lại xây dựng được một cái gì sao?

Bọn mình đã toan phóng ngay đến cái công trường kì dị ấy, nhưng ông cửa hàng trưởng nhắc hôm nay là ngày hội. Phải chờ đến mai mới được. Ông nói thêm:

• Nhân tiện hôm nay ở quán chúng tôi có một nhà ảo thuật trứ danh sắp biểu diễn. Các bạn có thích xem không?

Còn phải hỏi. Ai dại gì mà từ chối một dịp may như thế cơ chứ. Và cậu có tưởng tượng được không, người xuất hiện trên bục lại chính là nhà ảo thuật đã biểu diễn ở rạp xiếc nước Tí Hon dạo trước! Gặp lại anh ta, bọn mình mừng rỡ như được gặp lại người thân ấy. Chắc anh ta lại sắp biểu diễn cái trò chia số không thành một phần nghìn và giới thiệu bác Khổng Lồ từ nước Vô tận đến… nhưng không, mọi chuyện đều khác cả.

Nhà ảo thuật giơ tay lên, thế là không biết từ đâu ra một cái gậy dài. Anh ta buông gậy ra, nhưng gậy không rơi mà vẫn nằm lơ lửng trên không như nằm trên mặt bàn vậy. Nhà ảo thuật đề nghị người xem lên kiểm tra để tin chắc rằng cái gậy quả thực là tiện bằng gỗ liền một gióng chứ không phải là gậy giả.

Xê-va nhảy bổ lên bục trước nhất. Theo sau còn có mấy người xem nữa. Mọi người đều công nhận rằng đúng là gậy thật, không có lòe bịp gì.

Bấy giờ nhà ảo thuật mới vung tay một cái. Thế là một loạt số phụ việc của nhà ảo thuật nhảy tót lên đứng trên gậy giống như một đàn chim sẻ đậu trên dây điện vậy.

Nhà ảo thuật nói:

• Xin các bạn chú ý! Các số này xếp trên gậy theo một trật tự nhất định. Từ trái sang phải các số tăng dần lên, số sau lớn hơn số trước một lượng nhất định.
• Lớn hơn nhau hai đơn vị! – Cả phòng nhao nhao nói.
• Đúng! Lớn hơn hai đơn vị.

Nhà ảo thuật lại vung tay và trên gậy xuất hiện những số mới.

• Đề nghị người xem cho biết, trật tự trong dãy số này thế nào?
• Số sau lớn hơn số trước năm đơn vị. – Mình nói Nhà ảo thuật nghiêng mình:
• Xin cảm ơn bạn. Đúng thế. Và tôi xin thông báo để các bạn biết là, dãy số trong đó mỗi số đứng sau lớn hơn số đứng trước một đại lượng không đổi thì gọi là cấp số cộng. Đại lượng không đổi ấy gọi là công Còn bản thân các số thì gọi là số hạng của cấp số!
• A! Nghĩa là trong trường hợp thứ nhất công sai là hai, còn trong trường hợp thứ hai công sai là năm. – Có ai đó nhận xét như vậy.
• Giỏi lắm! – Nhà ảo thuật vỗ tay khuyến khích. Xê-va lấy khuỷu tay hích mình một cái:
• Cũng hay đấy. Nhưng bao giờ mới đến trò ảo thuật nhỉ?

Chắc nhà ảo thuật nghe tiếng. Anh ta hóm hỉnh nhìn Xê-va rồi lại vẫy tay. Cái gậy chắc nịch, tiện bằng gỗ liền một gióng bỗng gập làm đôi và chập hai đầu lại gần nhau. Bây giờ những số cách đều hai đầu gậy thành ra nằm đối diện nhau: ba đối diện với bốn mươi tám, tám đối diện với bốn mươi ba, v.v…

Nhà ảo thuật lên tiếng:

• Đề nghị các bạn cộng từng cặp số này lại. Bất kì cặp số nào cũng được.

Bọn mình cộng cặp số ba và bốn mươi tám. Được năm mươi mốt. Rồi lại cộng tám với bốn mươi ba.

Cũng được năm mươi mốt. Mười ba với ba mươi tám… Thế là thế nào nhỉ? Lại năm mươi mốt! Rồi mười tám với ba mươi ba, hai mươi ba với hai mươi tám – lần nào cũng được tổng là năm mươi mốt cả.

• Đúng là ảo thuật rồi! – Xê-va thốt lên.
• Ảo thuật đâu? – Nhà ảo thuật khoát – Thế mà bạn cho là ảo thuật ư? Hà, hà, hà! Chỉ là một qui tắc hết sức tầm thường của môn đại số học thôi.
• Thế thì ảo thuật ở chỗ nào mới được chứ? – Xê-va hùng hổ hỏi.

Nhà ảo thuật lơ đãng vuốt thẳng cái gậy ra, tựa hồ như cái gậy làm bằng giấy.

• Xin bạn hãy cứ thử đặt cái gậy nằm lơ lửng trong không trung. Sau đó gập nó làm đôi rồi lại vuốt thẳng nó ra xem nào. Thử xong chắc bạn sẽ chẳng hỏi vặn tôi như thế nữa đâu!

Mọi người cười ồ, vỗ tay ran. Nhà ảo thuật lại nói tiếp:

• Bây giờ các bạn cùng tôi làm một thí nghiệm nho nhỏ nhé. Xem bạn nào cộng tất cả các số của cấp số cộng này nhanh nhất? Một, hai, ba – bắt đầu!

Trong phòng nhộn lên tiếng xì xào, tiếng giấy sột soạt, tiếng bút chì miết trên giấy. Bọn mình cũng cộng gấp:

3 + 8 + 13 + 18 + 23 + 28 + 33 + 38 + 43 + 48

Thoạt tiên cộng nhầm, rồi cộng thêm cột. Nhưng có lẽ xúc động thế nào ấy nên cứ tính nhầm mãi. Thành thử muốn tính nhanh lại hóa ra chậm suýt nữa thì bọn mình quay ra cãi nhau.

Nhưng nhà ảo thuật đã giơ cao tay lên:

• Thôi! Các bạn tính lâu quá. Thế thì còn làm nên trò trống gì nữa. Có thể tính nhanh hơn nhiều. – Anh ta vừa gập đôi cái gậy lại vừa nói tiếp – Cứ xem đây khắc thấy tôi nói đúng! Ta có năm cặp số. Tổng mỗi cặp đều là năm mươi mốt, thì tổng của năm cặp phải lớn gấp năm lần hơn. Tôi đem năm mươi mốt nhân với năm. Được bao nhiêu nào? Hai trăm năm mươi nhăm! Bây giờ xin mời các bạn làm thử xem sao. Ai muốn thử, xin mời lên đây, đừng chen lấn nhau nhé!

Mình rất muốn thử nhưng cứ ngường ngượng thế nào ấy.

Nhưng Ô-lếch đã đẩy mình lên.

Lúc này, trên gậy xuất hiện những số khác:

Đề nghị bạn tìm tổng các số này, – nhà ảo thuật nói – Mau lên, mau lên!

Mình bèn nói ngay:

• Trong cấp số này có tám số hạng, tức là có bốn cặp. Tổng hai số hạng ngoài cùng là bốn mươi hai. Tôi nhân bốn mươi hai với bốn. Được một trăm sáu mươi tám. Có đúng không?
• Hoàn toàn đúng! – Nhà ảo thuật xác nhận. – Một trăm sáu mươi tám!
• Nhưng tại sao ở nước An-giép anh lại giải những bài toán của nước Tí Hon? – Xê-va hỏi xen vào. – Đây chỉ là một bài toán số học tầm thường thôi.
• Đúng! Một bài toán rất tầm thường, nhưng dùng cách trên chúng ta đã đơn giản hóa được cách giải. Xin bạn lưu ý cho rằng, đơn giản hóa là một trong những phương châm chính của nước An-giép. Một phương châm nữa là khái quát hóa. Quy tắc mà tôi vừa giới thiệu với các bạn có thể áp dụng cho bất kì cấp số cộng nào cũng được. Và do đó…
• Do đó có thể dùng chữ để biểu diễn, – Xê-va vội cắt lời nhà ảo thuật.
• Tuyệt lắm! – nhà ảo thuật khen. – Anh bạn nói rất đích đáng. Bây giờ tôi không xếp số mà xếp các chữ lên gậy. Mỗi số hạng của cấp số, tôi kí hiệu bằng một chữ a kèm thêm số thứ tự để khỏi lẫn. Số thứ tự ấy gọi là chỉ số và viết ở bên phải chữ, hơi thấp xuống một tí.

Nhà ảo thuật ra hiệu, thế là các chữ a kèm theo chỉ số nhảy phắt ngay lên đứng trên gậy.

Các bạn chú ý này! Tôi sẽ rút ra công thức đấy. Trong dãy số này a

₁

và a

₂

có thể hiểu ngầm là bất kì số nào cũng được cả.

• Dĩ nhiên rồi, – Xê-va vội nói. – Mọi số còn lại cũng đều như thế mà lị.
• Hãy suy nghĩ cho kĩ, anh bạn trẻ ạ! – nhà ảo thuật phản đối. – Các chữ a này là số hạng của một cấp số cộng đấy nhé. Cho nên chỉ có hai số a đầu tiên là có thể chọn tùy ý. Các số còn lại phải lệ thuộc vào hiệu giữa hai số đầu tiên. Tôi kí hiệu hiệu số ấy là d, vì trong một cấp số thì hiệu số ấy không thay đổi. Vậy tôi có

a₂ = a₁ + d a₃ = a₂ + d a₄ = a₃ + d

…

• Cứ thế cho đến cuối cấp số. Các bạn có hiểu không?
• Có! Có! – Mọi người nhao nhao trả lời.
• Tôi tiếp tục nhé! Tôi tin rằng tất cả các bạn đều thấy trong cấp số này có tám số hạng, hay bốn cặp. Tôi viết tổng các số hạng ngoài cùng là:

a₁ + a₈

• Nếu kí hiệu tổng các số hạng của cấp số là S thì tôi sẽ có S = 4(a₁ + a₈)

Có người hỏi:

• Nếu cấp số có mười số hạng thì tính thế nào?
• Cũng tính hệt như thế thôi, – nhà ảo thuật đáp. – Có điều bây giờ là năm cặp chứ không phải bốn cặp, và số hạng cuối cùng là a₁₀:

S = 5(a₁ + a₁₀)

• Thành ra qui tắc này áp dụng cho bất kì cấp số có bao nhiêu số hạng cũng được, có phải không? – Một khán giả thích tỉ mỉ lên tiếng hỏi.
• Thế các bạn thích cộng bao nhiêu số hạng nào?
• Năm! Hai mươi! Một trăm bảy mươi lăm! Hai trăm bốn mươi!

Một triệu bảy mươi vạn! – Bốn bề người ta nhao nhao nói.

Nhà ảo thuật lấy tay bịt tai:

• Trật tự! Trật tự! Tôi sẽ xin thỏa mãn tất cả yêu cầu của các bạn.

Anh ta chờ cho mọi người yên lặng rồi nói tiếp:

• Tôi kí hiệu số số hạng bằng chữ Số hạng cuối cùng của cặp số sẽ là a_n và tổng các số hạng ngoài cùng là:

a₁ + a_n

• Chẳng khó khăn gì mà không đoán được rằng số cặp sẽ bằng nửa n, tức là . Thành ra, tổng các số hạng sẽ là

Xin hỏi, – Ô-lếch nói, – nếu số số hạng của cấp số là lẻ thì chia thành cặp như thế nào?
• À, chuyện ấy bạn thử tự nghĩ lấy xem Nhưng hãy tin vào lời nói trung thực của nhà ảo thuật là: công thức trên vẫn không có gì thay đổi đâu.

Nhà ảo thuật lại bẻ gập cái gậy một lần nữa, và cái gậy liền biến mất. Mọi người vỗ tay ran và cười hể hả. Nhà ảo thuật cũng gập người làm đôi và biến đi đột ngột như cái gậy của anh ta vậy.

Đấy, ở An-giép bọn mình được xem những trò ảo thuật như

vậy đấy.

Ta-nhi-a